


Next: Other (Dis-)Similarity Measures
Up: Similarity Measures for Document
Previous: Pearson Correlation
Contents
Extended Jaccard Similarity
The binary Jaccard coefficient measures the degree of overlap between
two sets and is computed as the ratio of the number of shared
attributes (words) of
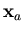 AND
AND
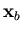 to
the number possessed by
to
the number possessed by
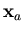 OR
OR
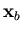 . For example, given two sets' binary indicator vectors
. For example, given two sets' binary indicator vectors
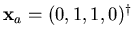 and
and
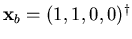 , the cardinality of their intersect is 1 and the
cardinality of their union is 3, rendering their Jaccard coefficient
1/3. The binary Jaccard coefficient It is often used in retail
market-basket applications. In chapter 3, we extended the binary definition of Jaccard
coefficient to continuous or discrete non-negative features. The
extended Jaccard is computed as
, the cardinality of their intersect is 1 and the
cardinality of their union is 3, rendering their Jaccard coefficient
1/3. The binary Jaccard coefficient It is often used in retail
market-basket applications. In chapter 3, we extended the binary definition of Jaccard
coefficient to continuous or discrete non-negative features. The
extended Jaccard is computed as
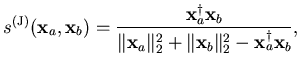 |
(4.4) |
which is equivalent to the binary version when the feature vector
entries are binary. Extended Jaccard similarity [SG00c]
retains the sparsity property of the cosine while allowing
discrimination of collinear vectors as we will show in the following
subsection. Another similarity measure highly related to the extended
Jaccard is the Dice coefficient (
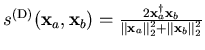 ). The Dice coefficient can be obtained from the extended Jaccard
coefficient by adding
). The Dice coefficient can be obtained from the extended Jaccard
coefficient by adding
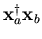 to both
the numerator and denominator. It is omitted here since it behaves
very similar to the extended Jaccard coefficient.
to both
the numerator and denominator. It is omitted here since it behaves
very similar to the extended Jaccard coefficient.



Next: Other (Dis-)Similarity Measures
Up: Similarity Measures for Document
Previous: Pearson Correlation
Contents
Alexander Strehl
2002-05-03
![]() AND
AND
![]() to
the number possessed by
to
the number possessed by
![]() OR
OR
![]() . For example, given two sets' binary indicator vectors
. For example, given two sets' binary indicator vectors
![]() and
and
![]() , the cardinality of their intersect is 1 and the
cardinality of their union is 3, rendering their Jaccard coefficient
1/3. The binary Jaccard coefficient It is often used in retail
market-basket applications. In chapter 3, we extended the binary definition of Jaccard
coefficient to continuous or discrete non-negative features. The
extended Jaccard is computed as
, the cardinality of their intersect is 1 and the
cardinality of their union is 3, rendering their Jaccard coefficient
1/3. The binary Jaccard coefficient It is often used in retail
market-basket applications. In chapter 3, we extended the binary definition of Jaccard
coefficient to continuous or discrete non-negative features. The
extended Jaccard is computed as
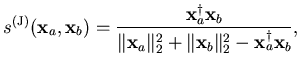
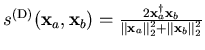 ). The Dice coefficient can be obtained from the extended Jaccard
coefficient by adding
). The Dice coefficient can be obtained from the extended Jaccard
coefficient by adding